La disyunción es otro símbolo
matemático perteneciente a los conectivos lógicos
cuya representación es una (V) normal. También este
conectivo tendrá su significado propio en las oraciones.
La disyunción reemplazara la Vocal O en las
proposiciones y por ende se llega a la conclusión de que
el valor de (v) = O y se leerá tal como la
vocal
c) Implicación (?)
La implicación es uno de los conectivos mas
importantes ya que tiene mas valor que la conjuncion y la
disyunción su simbología matemática es una
flecha (?) es un conectivo que tiene varios significados y por
ende habrá que prestarle un poco mas de atención.
Reemplazara las palabras Entonces, Luego, Por ende. Por tanto
Etc.
En las proposiciones y por ende se llega a la
conclusión de que el símbolo (?) tendrá
varios significados y se leerá conforma a la palabra que
reemplacé.
d) Doble Implicación
(?)
La Doble Implicación es un conectivo mas fuerte
que la implicación y por ende mas fuerte que la
disyunción y conjuncion su símbolo
matemático es (?). Tiene su significado correspondiente
dentro de las oraciones reemplazara a la palabra Si y Solo
Si en las proposiciones y se leerá tal como se lea
dicha palabra.
e) Disyunción Exclusiva
(V)
La disyunción exclusiva dentro de la
jerarquía de los conectivos viene a ocupar el primer
lugar. Su simbología matemática es una (v) Normal
que a diferencia de la disyunción tiene una línea
debajo de la (V) lo que por lo tanto permite diferenciarlas.
Reemplazara en las oraciones a la palabra O p O q Pero no
ambas lo que implica que se tendrá que elegir una sola
opción y no las dos al mismo tiempo. Se leerá tal
como se pronuncie la palabra correspondiente.
Valores de Verdad
de Una Proposición
El valor de verdad de una proposición tiene por
objetivo demostrar con que valor de verdad esta actuando una
proposición. Este valor puede ser verdadero o falso
dependiendo de la veracidad de dicha oración. Se simboliza
de la siguiente manera tomando el siguiente
significado.
? (P) = F o V "Significa el valor de
verdad de la proposición P es igual a F o
V"
PROBLEMAS QUE INVOLUCRAN
RESOLUCIONES CON PROPOSICIONES
a) PROBLEMA TIPO I (Dada una
Oración Determinar si es
Proposición)
– Determinar si las siguientes Oraciones
son Proposiciones
1.- la Gravedad vale
9,81 mt/sg2
Solución
1er paso.- Verificando que tipo de
oración es
Es una declaración
Declarativa
2do Paso.- Determinar si es
Proposición
Es una Proposición por que es una
declaración declarativa y por lo tanto se puede decir si
es verdadera o falsa
2.- 3+3=9
Solución
1er paso.- Verificando que tipo de
oración es
Es una declaración
Declarativa
2do Paso.- Determinar si es
Proposición
Es una Proposición por que es una
declaración declarativa y por lo tanto se puede decir si
es verdadera o falsa
3.- Algebra es una
materia de primer semestre
Solución
1er paso.- Verificando que tipo de
oración es
Es una declaración
Declarativa
2do Paso.- Determinar si es
Proposición
Es una Proposición por que es una
declaración declarativa y por lo tanto se puede decir si
es verdadera o falsa
4.- el cielo es de color
celeste
Solución
1er paso.- Verificando que tipo de
oración es
Es una declaración
Declarativa
2do Paso.- Determinar si es
Proposición
Es una Proposición por que es una
declaración declarativa y por lo tanto se puede decir si
es verdadera o falsa
5.- newton fue un famoso
químico
Solución
1er paso.- Verificando que tipo de
oración es
Es una declaración
Declarativa
2do Paso.- Determinar si es
Proposición
Es una Proposición por que es una
declaración declarativa y por lo tanto se puede decir si
es verdadera o falsa
6.- La carrera de
Ingeniería Petrolera pertenece a la facultad de Ciencias
Económicas
Solución
1er paso.- Verificando que tipo de
oración es
Es una declaración
Declarativa
2do Paso.- Determinar si es
Proposición
Es una Proposición por que es una
declaración declarativa y por lo tanto se puede decir si
es verdadera o falsa
7.- La materia de
algebra I es una materia muy difícil
Solución
1er paso.- Verificando que tipo de
oración es
Es una declaración
Declarativa
2do Paso.- Determinar si es
Proposición
Es una Proposición por que es una
declaración declarativa y por lo tanto se puede decir si
es verdadera o falsa
8.- las vocales son
diez
Solución
1er paso.- Verificando que tipo de
oración es
Es una declaración
Declarativa
2do Paso.- Determinar si es
Proposición
Es una Proposición por que es una
declaración declarativa y por lo tanto se puede decir si
es verdadera o falsa
9.- El tema de Derivadas
pertenece a la materia de Ecuaciones Diferenciales
Solución
1er paso.- Verificando que tipo de
oración es
Es una declaración
Declarativa
2do Paso.- Determinar si es
Proposición
Es una Proposición por que es una
declaración declarativa y por lo tanto se puede decir si
es verdadera o falsa
10.- En el curso existen
más de 100 Alumnos
Solución
1er paso.- Verificando que tipo de
oración es
Es una declaración
Declarativa
2do Paso.- Determinar si es
Proposición
Es una Proposición por que es una
declaración declarativa y por lo tanto se puede decir si
es verdadera o falsa
11.- 3+3
Solución
1er Paso.- Verificando que tipo de
oración es
Es una expresión
Matemática sin sentido
2do Paso.- Determinar si es
Proposición
No es una proposición por que
carece de igualdad por lo tanto no se puede decir si es verdadera
o falsa.
12.- Quiero ir a la
Plaza
Solución
1er Paso.- Verificando que tipo de
oración es
Es una oración de
deseo
2do Paso.- Determinar si es
Proposición
No es una proposición por que es
una oración de Deseo y por lo tanto no tiene sentido
afirmar si es verdadera o falsa
13.- Quiero Jugar
Cartas
Solución
1er Paso.- Verificando que tipo de
oración es
Es una oración de
deseo
2do Paso.- Determinar si es
Proposición
No es una proposición por que es
una oración de Deseo y por lo tanto no tiene sentido
afirmar si es verdadera o falsa
14.- Tráeme dos
asientos del otro curso por favor
Solución
1er Paso.- Verificando que tipo de
Oración es
Es una oración de
Orden
2do Paso.- Determinar si es
Proposición
No es una Proposición por que es
una oración de orden y por lo tanto no tiene sentido
afirmar si es verdadera o falsa
15.- Ayúdame a
terminar mi tarea
Solución
1er Paso.- Verificando que tipo de
Oración es
Es una oración de
Orden
2do Paso.- Determinar si es
Proposición
No es una Proposición por que es
una oración de orden y por lo tanto no tiene sentido
afirmar si es verdadera o falsa
16.- ¡Viva
Blooming!
Solución
1er Paso.- Verificando que tipo de
Oración es
Es una oración de
Admiración
2do Paso.- Determinar si es
Proposición
No es una Proposición por que es
una oración de Admiración y por lo tanto no tiene
sentido afirmar si es verdadera o falsa.
17.- ¡Viva Santa
Cruz!
Solución
1er Paso.- Verificando que tipo de
Oración es
Es una oración de
Admiración
2do Paso.- Determinar si es
Proposición
No es una Proposición por que es
una oración de Admiración y por lo tanto no tiene
sentido afirmar si es verdadera o falsa
18.- ¿Cómo
es tu Nombre?
Solución
1er Paso.- Verificando que tipo de
Oración es
Es una oración de
Interrogación
2do Paso.- Determinar si es
Proposición
No es una Proposición por que es
una oración de Interrogación y por lo tanto no
tiene sentido afirmar si es verdadera o falsa
19.-
¿Cuántos años tienes?
Solución
1er Paso.- Verificando que tipo de
Oración es
Es una oración de
Interrogación
2do Paso.- Determinar si es
Proposición
No es una Proposición por que es
una oración de Interrogación y por lo tanto no
tiene sentido afirmar si es verdadera o falsa
20.- ¿Cuál
es tu materia Favorita?
Solución
1er Paso.- Verificando que tipo de
Oración es
Es una oración de
Interrogación
2do Paso.- Determinar si es
Proposición
No es una Proposición por que es
una oración de Interrogación y por lo tanto no
tiene sentido afirmar si es verdadera o falsa
b) PROBLEMA TIPO II (Dadas las
proposiciones determinar su expresión
simbólica)
– Para solucionar estos problemas se
siguen los siguientes pasos
1.- Se lee el pensamiento para
determinar cuantas oraciones tiene el mismo
2.- El numero de oraciones estará
en función a los conectivos lógicos que se
encuentren en el pensamiento es decir y-o-entonces-si y solo si-
si P o Q pero no ambas. (Palabras claves)
3.- Una vez determinado el número
de oraciones existentes en el pensamiento se procede a nombrar a
cada una asignándole un valor a cada una generalmente una
letra del alfabeto a partir de la letra P.
4.- Si hubiera oraciones negadas estas
deben nombrarse en forma positiva y cuando se tengan que
simbolizar se las coloca en forma negativa.
5.- Se procede a escribir el pensamiento
en su correspondiente simbología matemática
reemplazando las palabras claves por sus respectivos
conectivos
NOTA: EN LOS EJERCICIOS A CONTINUACION
EL COLOR ROJO MOSTRARA LOS CONECTIVOS QUE SE ENCUENTRAN EN CADA
ORACION.
21.- No es cierto que no me gusta
bailar
* Solución
* Asignando un valor a la
Oración
p = Me gusta bailar
* Formalizando la
Oración
~~p
22.- Me gusta bailar y leer libros de
ciencia ficción
* Solución
* Asignando un valor para cada
Oración
p = Me gusta bailar
q = Leer libros de ciencia
ficción




PROBLEMA TIPO III (Dadas las
proposiciones y su simbología correspondiente determinar
su correspondiente en lenguaje común)
1.- Se reemplaza los valores
correspondientes asignados a cada proposición donde
corresponda.
2.- Se procede a escribir su
equivalencia en lenguaje comun
Sean p, q y r los siguientes
enunciados:
p = Estudiare
Matemáticas
q = Iré a mi clase de
Computación
r = Estoy de buen humor
Escriba en lenguaje común las
oraciones que correspondan a los siguientes
enunciados

* Solución
* Colocando el valor correspondiente a
cada proposición
p = Estudiare
Matemáticas
q = Iré a mi clase de
Computación
* Encontrando su correspondiente en
lenguaje común


* Solución
* Colocando el valor correspondiente a
cada proposición
p = Estudiare
Matemáticas
q = Iré a mi clase de
Computación
r = Estoy de buen humor
* Encontrando su correspondiente en
lenguaje común

Para los problemas tipo IV, V, VI se
necesitara primero hacer una pequeña introducción a
los valores de verdad de cada conectivo lógicos para que
de esta manera se entienda mejor como se solucionan estos
problemas
TABLA DE VALORES DE LOS
CONECTIVOS LOGICOS
1.- CONJUNCION
(^)

La conjuncion es verdadera solamente
cuando el antecedente p y el consecuente q son también
verdaderos como se muestra en su tabla marcado con el color
rojo
2.- DISYUNCION
(V)

La disyunción es falsa solamente
cuando el antecedente p y el consecuente q son también
falsos como se muestra en su tabla marcado con el color
rojo
3.- IMPLICACION
(?)

La implicación es falsa solamente
cuando el antecedente p es verdadero y el consecuente q es falso
como se muestra en su tabla con el color rojo
4.- BICONDICIONAL O
DOBLE IMPLICACION (?)

La doble implicación tiene dos
casos especiales será verdadera cuando el antecedente p y
el consecuente q tomen ambos valores idénticos como se
muestra en su tabla marcado con el color rojo
5.- DISYUNCION EXCLUSIVA
(V)

La disyunción exclusiva resulta
ser la negación de la doble implicación ya que
será falsa cuando el antecedente p y el consecuente q
tomen ambos a la vez valores idénticos como se demuestra
con rojo en su tabla de verdad.
FORMULARIO PARA FACIL
RESOLUCION DE LOS PROBLEMAS
Para evitar de aprenderse todas las
combinaciones mostradas en cada una de las tablas de verdad de
los conectivos lógicos se realizara este formulario que
permitirá una fácil solución de los
problemas

Por lo tanto el alumno solo debe
aprenderse estas siete combinaciones para poder dominar y
resolver los problemas que se mostraran a
continuación
PROBLEMA TIPO IV (VALORES DE VERDAD CON
CONDICIONES)

* Solución
* Encontrando el valor de las
proposiciones cualesquiera
Como las variables q y s son
proposiciones cualesquiera esto significa entonces de que
nosotros podemos elegir en forma voluntaria el valor que tomara q
y s
Por lo tanto elegimos de qué q
sea V y s sea F:
q = V
s = F
* Análisis de la
condición
El problema tiene una condición
la cual es ~ (p ? ~ r) es verdadera significa entonces de que las
variables p y r no pueden ser elegidas por nosotros sus valores
saldrán de resolver la condición expuesta en el
ejercicio
Como se resuelve la
condición?
Reemplazando un valor a la variable p y
a la variable r de tal manera que cuando se hagan operaciones
esta de cómo resultado verdadero aquí entra la
aplicación del formulario expuesto
anteriormente.

Por lo tanto para que la
conclusión se cumpla Las variables p y r deben tomar los
siguientes valores
p = F
r = V
* Reemplazando para encontrar el valor
de verdad correspondiente
Como ya hemos encontrado todos los
valores correspondientes a las proposiciones procedemos a
reemplazarlas en la proposición para encontrar su valor de
verdad

* Solución
Como el problema tiene la misma
condición del problema anterior entonces ya conocemos
cuanto valen los valores de verdad de cada
proposición
p = F
q = V
r = V
s = F
* Reemplazando para encontrar el valor
de verdad








Introducción a las tablas de
verdad

Es una
CONTINGENCIA

Es una
CONTINGENCIA

Es una
TAUTOLOGIA

Es una
CONTRADICCION

Es una
TAUTOLOGIA

Es una
CONTINGENCIA

Es una
ANTITAUTOLOGIA

* Es una
TAUTOLOGIA

Es una
CONTINGENCIA

Es una
CONTINGENCIA
La fórmula que rige las tablas de
verdad está en función a la cantidad de letras o
variables que tenga la proposición esta fórmula
está representada por la siguiente expresión
matemática:

Donde n es la cantidad de variables o
letras que posea la formula proposicional, cabe recordar que el
número de proposiciones puede ser ilimitado, lo que
significa que las tablas de verdad pueden determinar el valor de
verdad de cualquier razonamiento lógico sin importar el
número de variables que tenga dicho razonamiento, es
también importante mencionar que el razonamiento estudiado
mediante una tabla de verdad no debe ser cualquiera si no uno que
tenga y cumpla con las leyes de la lógica, es decir un
pensamiento que tenga claridad y que indique algo aproximado a la
realidad.

Es una
CONTINGENCIA
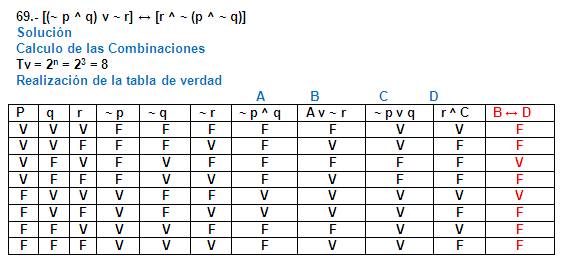
Es una
CONTINGENCIA
Las letras A, B, C etc. que se ven en la parte superior
de algunos ejercicios son conocidas como "Auxiliares o pivotes"
ya que permiten resumir la realización de un ejercicio es
decir pueden representar a una formula extensa que exista en la
proposición se colocan encima de la formula a la cual
están representando así se sabrá que formula
fue designada por una de estas letras en la proposición
evitando una solución larga.

Es una
CONTINGENCIA
SIMPLIFICAR LAS PROPOSICIONES
SIGUIENTES:

















109.- Demostrar la validez de los
siguientes razonamientos
Si la ballena es un mamífero
entonces toma oxigeno del aire. Si toma oxigeno del aire entonces
no necesita branquias. La ballena es un mamífero y habita
en el océano. Por tanto, habita en el océano y no
necesita branquias.
* Solución
* Asignándole un valor a cada
proposición
p = Si la ballena es un
mamífero
q = Toma oxigeno del aire
r = Necesita branquias
s = Habita en el océano
* Transformando a su expresión
Lógica

110.- Demostrar la validez de los
siguientes razonamientos
Si la enmienda no fue aprobada entonces la
constitución queda como estaba. Si la constitución
queda como estaba, entonces no podemos añadir nuevos
miembros al comité. Podemos añadir nuevos miembros
al comité o el informe se retrasara un mes. Pero el
informe no se retrasara un mes. Por tanto la enmienda fue
aproada.
* Solución
* Asignándole un valor ara cada
Proposición
p = Si la enmienda fue aprobada
q = La constitución queda como
estaba
r = Podemos añadir nuevos miembros
al comité
s = El informe se retrasara un
mes
* Transformando a su expresión
lógica
Demostrar: p (Método
Directo)

111.- Demostrar la validez de los
siguientes razonamientos
Si el reloj esta adelantado entonces Juan llego antes
de las diez y vio partir el coche de Andrés. Si
Andrés dice la verdad, entonces Juan no vio partir el
coche de Andrés. Andrés dice la verdad o estaba en
el edificio en el momento del crimen. El reloj esta adelantado.
Por tanto, Andrés estaba en el edificio en el momento del
crimen.
* Solución
* Asignándole un valor a cada
Proposición
p = Si el reloj esta adelantado
q = Juan llego antes de las diez
r = Vio partir el coche de
Andrés
s= Andrés dice la verdad
t= Estaba en el edificio en el momento del
crimen
* Transformando a su expresión
lógica
Demostrar: t (Método
Directo)

112.- Demostrar la validez de los siguientes
razonamientos
Si Marcos consigue trabajo entonces comprara un
automóvil. Si Marcos compra un automóvil entonces
no conducirá con cuidado. Si Marcos no conduce con cuidado
entonces tendrá un accidente.
Por tanto: Si Marcos consigue trabajo entonces
tendrá un accidente
* Solución
* Asignándole un valor a cada
Proposición
p = Marcos consigue trabajo
q = Comprara un automóvil
r = Conducirá con cuidado
s = Tendrá un accidente

114.- Demostrar: ~ p Método
Indirecto
















Autor:
Francisco
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |